[프로그래머스] 조이스틱 & 백준 3663번 (with python3)

Computer Science/알고리즘

[프로그래머스] 조이스틱 & 백준 3663번 (with python3)

highcastlee 2021. 8. 6. 03:44

Background

- 해당 문제는 프로그래머스에서는 그리디 알고리즘으로 분류되어 있지만,

실제 풀이에서는 그리디 + 완전 탐색에 가깝다.

문제

Test Case

test	Parameters	Return
1	"JEROEN"	56
2	"JAN"	23
3	(추가) "ABAAAAABBA"	8
4	(추가) "AABAAAABBB"	11
5	(추가) "AABAAAAAAB"	6 (백준 기준)

*핵심 포인트

시작점 : 0번 인덱스

1번 케이스 : [정방향] 커서 이동

2번 케이스 : [역방향] 커서 이동

3번 케이스 : [정방향] 후 [역방향] 커서 이동

4번 케이스 : [정방향] 후 [역방향] 커서 이동

5번 케이스 : [역방향] 후 [정방향] 커서 이동

*정방향 : 왼쪽 -> 오른쪽

Point 1) 요구사항 체크

- 문제의 요구사항을 보면, 첫 번째 위치에서 왼쪽으로 이동하면 마지막 위치로 가지만, 마지막 위치에서 오른쪽으로 이동하면 첫 번째 위치로 간다는 말은 언급하지 않았다. (백준 3663번은 동일 문제이지만, 좌우 이동 자유)

+ 이게 포인트인 이유는, 테스트 케이스 5번에서 [역방향] 후 [정방향]일 경우, 최소 조이스틱 횟수가 6번이지만, 문제의 요구사항에 따라 [정방향] 후 [역방향]으로 진행한다면 최솟값은 7번이 된다.

Point 2) 잘못된 코드의 통과

- 몇몇 블로그의 풀이에서는 단순히 양방향으로 다음 'A'가 없을 때까지의 index를 비교해서 더 짧은 거리의 방향으로 진행하도록 코드를 작성했지만, 그 방법은 테스트 케이스 4번에서 [마지막 위치 => 첫 위치] 조건이 필요하고, 최솟값이 11이 아닌 12가 나오게 된다. (방향 조건도, 최솟값도 틀린 이 케이스를 프로그래머스에서는 그냥 통과되도록 되어 있어서 잘못된 풀이 방법을 블로그에 작성해놓은 분들이 많다.)

잠정 결론) 해당 프로그래머스 문제의 출처는 백준 3663번처럼 좌우 오버 이동이 모두 가능하다. 그럼 방향 조건 상관없이 최소 거리를 구하면 되는데, 엄밀히 따지면 다른 문제인 프로그래머스의 채점 케이스에서 백준 문제의 solution이 통과되기 때문에 프로그래머스가 해당 출처의 문제를 변형하면서 조건을 명확하게 하지 않은게 본질적 문제인 듯하다.

즉, 프로그래머스의 조이스틱 문제 및 TC가 약간 못난 것 같으니, 그냥 백준 3663번을 기준으로 풀이를 작성한다.

풀이 방법 (좌우 오버 이동 가능한 최소 거리 합 구하기)

- 먼저, 필요한 작업은 크게 두 가지로 나눌 수 있다.

작업 1) 조이스틱 위아래 조작 Count : name[index]의 알파벳과 'A'와의 차이 구하기

방법 (1) 26개인 각 알파벳과 A와의 차이를 배열화 및 아스키코드 차이를 index로 활용 [A - Z]

ex. num_char = [0, 1, 2, 3, .... , 12, 13, 12, .... , 3, 2, 1] 활용

방법 (2) 'A'와 특정 알파벳의 아스키코드 차이를 좌우 방향으로 비교하여 최솟값 구하기

작업 2) 조이스틱 좌우 조작 Count : name 중 'A'가 아닌 위치로 이동할 때의 거리 합 중 최솟값

Test Case 1 : "JEROEN" >> [정방향]으로만 이동

Test Case 2 : "JAN" >> [역방향]으로만 이동

Test Case 3 : "ABAAAAABBA" >> [정방향] 후 [역방향] 커서 이동

Test Case 4 : "AABAAAABBB" >> [정방향] 후 [역방향] 커서 이동

Test Case 5 : "AABAAAAAAB" >> [역방향] 후 [정방향] 커서 이동

//프로그래머스 내 신동주님 풀이
def solution(name):
    answer = 0
    n = len(name)

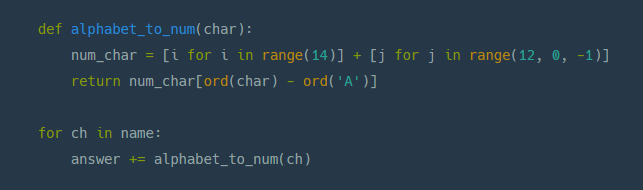
    def alphabet_to_num(char):
        num_char = [i for i in range(14)] + [j for j in range(12, 0, -1)]
        return num_char[ord(char) - ord('A')]

    for ch in name:
        answer += alphabet_to_num(ch)

    move = n - 1
    for idx in range(n):
        next_idx = idx + 1
        while (next_idx < n) and (name[next_idx] == 'A'):
            next_idx += 1
        distance = min(idx, n - next_idx)
        move = min(move, idx + n - next_idx + distance)

    answer += move
    return answer

위 코드를 이해하려면 [idx], [next_idx], [n - next_idx], [distance], [move]가 어떤 의미인지 알아야한다.

풀이의 핵심은 중복 이동을 역방향에서 할 것인지, 정방향에서 할 것인지 결정하는 것인데,

● move 초기 값은 방향 전환 없이 정방향일 경우, n-1이다.

- while 조건문을 통해 'A'가 연속일 경우, next_idx는 최대 n까지 증가한다. (n - next_idx = 0 이 됨)

- 따라서, 'ABBAAAA' 같은 케이스에서도 정방향 거리로 최솟값이 성립할 수 있다.

while (next_idx < n) and (name[next_idx] == 'A'):
      next_idx += 1

● idx는 'A'가 아닌 첫 알파벳을 찾기 위함이고,

● next_idx는 'A'가 아닌 마지막 알파벳을 찾기 위함이다. (완전 탐색에 가깝다..)

● (n - next_idx)는 첫 위치에서 마지막 알파벳까지 역방향 거리를 의미한다.

● distance는 idx와 n-next_idx 중 더 짧은 방향에서 2번 이동하기 위해 구하는 값이다.

● move는 idx 및 n-next_idx 에 추가로 더 짧은 distance를 중복으로 더해주는 값이다.